Harmonising the Major Scale

When we use the phrase ‘harmonising the major scale’, what we really mean is ‘building chords’. When we harmonise the major scale, we build a chord from each note of the scale.

What is a chord?

A chord, technically, is the combination of three or more notes. A straight major or minor chord has only 3 separate notes. Often we strum major or minor chords on the guitar which use more than 3 strings. Even though we are playing 4, 5, or even 6 strings, we are only playing 3 individual notes which are doubled in different octaves.

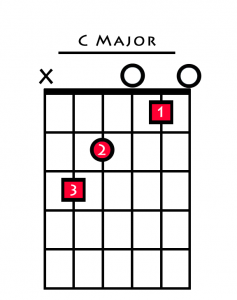
For example in the following chord of C major the names of the notes are labelled… You can see that even though we play 6 strings, there are only 3 unique notes.

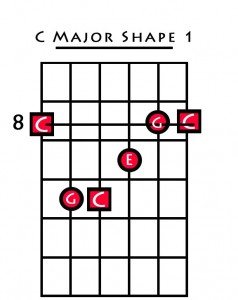
In this voicing, the note C appears 3 times, and the note G appears twice. The only note to appear once is the E.

Where do these notes come from?

To find out which notes go together to form each individual chord, we must learn how to go about harmonising the major scale.

Chords are formed when we ‘stack’ specific notes from a scale on top of each other. Look again at the previous example. The chord of C Major contains only the notes, C, E and G. In the context of the major scale, we have taken the notes 1, 3 and 5:

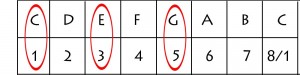
This can be seen as jumping over or ‘leapfrogging’ every other note in the scale. For example, we formed this chord by Starting on C, Jumping D and landing on E, jumping F and landing on G. This is how most simple, 3 note chords are formed.

1) C E G

2) D F A

3) E G B

4) F A C

5) G B D

6) A C E

7) B D F

If we look at the notes of C major spaced out on the fret board, we can now establish what pattern of notes is required to form a major chord.

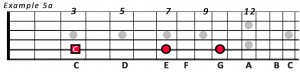
The distance between the notes C and E is two tones.

Any chord with a distance of two tones between the first two notes can be classed as a major type chord. This distance in music is called a ‘major 3rd’.

The distance between the 3rd and 5th (the notes E and G), is one and a half tones. This is one semitone smaller than the major 3rd so we call it a minor 3rd.

When measured from the root, any major chord must consist of 2 tones between the root and 3rd, and 3.5 tones between the root and 5th.

It is convention in music to describe the notes in a chord in terms of their relationship to the major scale formula, 1 2 3 4 5 6 7.

So, in simple terms a major chord has the formula 1 3 5 and the first chord in any major key is always major.

Moving on to the second note in the C major scale, (D) and repeating the previous process we generate:

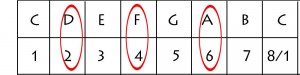
As we start harmonising the major scale from the 2nd note of the scale, we get the notes D, F and A. On the guitar, that looks and sounds like:

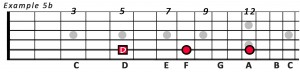
The distance between the notes D and F is 1.5 tones or a minor 3rd which means that the chord is minor.

However; the distance between the notes D and A is still 3.5 tones, which is the correct spacing for a perfect 5th.

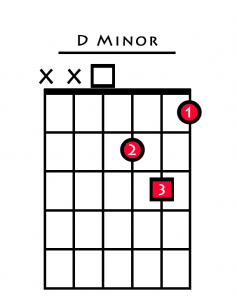
With a minor 3rd and a perfect 5th, this chord is classified as a minor chord built on the note D, or simply ‘D minor’ for short.

As a formula, a minor chord is expressed as 1 b3 5 and the second chord in any major key is always minor.

All the notes of the major scale can be harmonised in this way, and with the exception of the 7th note, B, they are all normal major or minor chords.

To save space I will not show the construction of every chord (although do try this by yourself). The harmonised chords of the C major scale are:

Chord 1 (I)	C Major
Chord 2 (ii)	D Minor
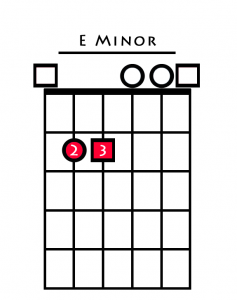
Chord 3 (iii)	E Minor
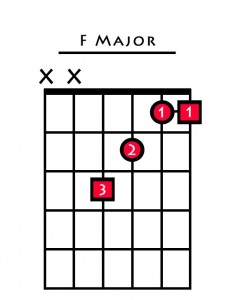
Chord 4 (IV)	F Major
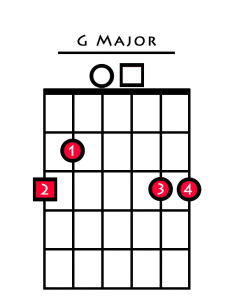
Chord 5 (V)	G Major
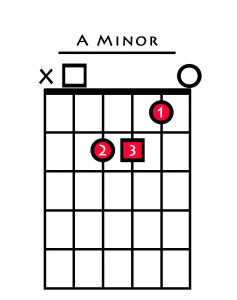
Chord 6 (vi)	A Minor
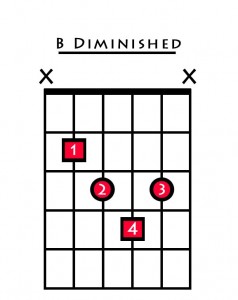
Chord 7 (vii)	B Minor (b5) or B Diminished

Harmonising the 7th Degree of the Major Scale

The 7th or leading note, B is different. It is the only chord that does not contain a perfect fifth. When we harmonise the 7th degree of a major scale, the 5th is one semitone smaller and is called a diminished fifth, or b5 for short.

This can be seen and heard in example 5c

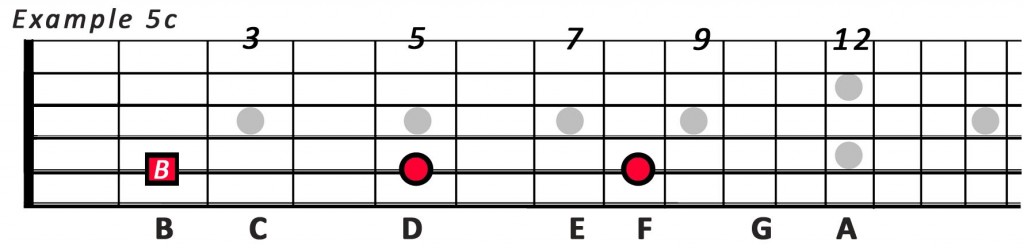
The distance between the notes B and D is a minor 3rd so this must be some type of minor chord. However; the distance between the notes B and F is only 6 semitones, not 7 as in the previous examples. This chord is therefore named B minor(b5) or B Diminished. The chord is played like this:

Example 5d

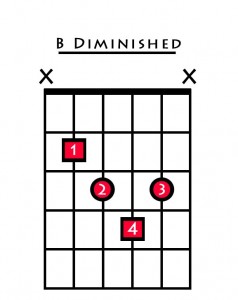
This is the only chord in major scale harmony that has not got a perfect 5th. It is not often used in pop music due to its dissonant nature. When it is used, it is normally a substitution for the 5th chord of the scale.

The Roman Numeral System

In music, chords are often referred to by the Roman numeral numbering system. Instead of labelling them 1, 2, 3, 4, 5, etc, they are given the Roman numeral equivalent numbers.

1 = I, 2 = ii, 3 = iii, 4 = IV, 5 = V, 6 = vi, 7 = vii.

This is to avoid confusion when we’re talking about interval distances: 3rds, 4ths and 5ths, and chords: iii, IV or V

You will notice that sometimes I have used capital letters for each numeral, and sometimes lower case letters. We use capital letters to describe major chords and lower case letters to describe minor chords.

You can see that in a major key, chords I, IV and V are always major, whereas ii, iii, vi and vii are minor.